1月5日，罗莎·温特(Rosa Winter)将获得算术几何博士学位。她研究了定义所谓“ del Pezzo曲面”的方程式的解决方案。“温特说：“我喜欢几何，因为我可以想象并绘制形状和对象。这使抽象数学感觉更切实。

在数学中，有时使用诸如圆形，球形，八面体甚至更高维的物体之类的几何物体来研究抽象方程是有用的。将几何图形与抽象方程式连接的字段称为算术几何图形。博士 候选人罗莎·温特(Rosa Winter)在论文中运用了这种特定类型的几何图形。

图纸表面

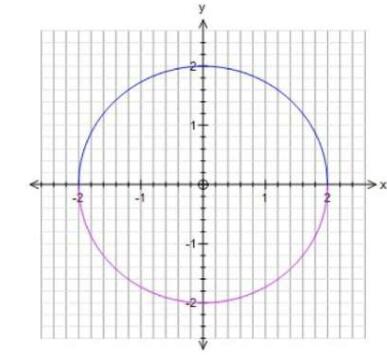
数学方程可以定义几何对象，这意味着可以使用几何来研究这些方程的解。例如，如果您想知道可以输入哪些数字以使x ^ 2 + y ^ 2等于4，则可以绘制x ^ 2 + y ^ 2 = 4的所有点(解)。这将产生一个半径为2的圆，例如，它表明点x = 2，y = 0是一个解。您还可以寻找特定的解决方案，例如x和y为分数(1 / 3、1 / 5，但也为0、2等)的圆上的点。这些分数解称为有理点。温特研究了表面上的有理点。温特说：“表面始终是二维的，即使它们存在于八个维度中也是如此。” “这意味着我可以绘制表面，从而使抽象数学对我来说更直观。”

百万美元的问题

在几何对象上找到有理点很少很容易。例如，这就是所谓的“伯奇和斯温纳顿-代尔猜想”。这个尚未得到证实的数学猜想是“千禧奖问题”的一部分。克莱数学研究所(Clay Mathematics Institute)奖励一百万美元，以解决这些问题中的任何一个。该猜想是关于椭圆曲线上的有理点的。像圆一样，椭圆曲线是由某些方程式定义的几何对象。当您绘制它们时，它们看起来像曲线。温特：“即使是众所周知的椭圆曲线，要确定有理点的集合也不容易。”

Del Pezzo表面

不幸的是，温特在攻读博士学位期间没有收集到一百万美元。研究。她没有在椭圆曲线上的有理点上工作，而是在所谓的1度'del Pezzo曲面上工作。” Winter：“从几何角度来看，这些不是最困难，最复杂的曲面，但它们仍然没有答案她证明了该系列曲面的一部分包含无限数量的不聚集的有理点;它们可以散布在表面周围。如果有理点以红点的形式可见，则您可以穿过这些点在del-Pezzo曲面上，您到处都会看到红色有理点。

自9月以来，温特一直在莱比锡的马克斯·普朗克数学科学研究所担任博士后。在这里，她学习了如何在其他科学(例如生物学和物理学)中应用几何和抽象数学。